Options Strategy – Dividends & Put-Call Parity
Video Tutorial
beeTrader – Dividendi & Put-Call Parity
Premise: it is essential to know the exact price of the underlying to which the options refer and therefore their moneyness (position with respect to the price of the underlying). In cases where there are future changes in the price of the underlying it is necessary to consider this change because the moneyness of the options on the subsequent expiries will be different from the current one. Dividend dividends lower the value of the financial instrument, index or stock, which has detached them.
In a market with continuous bargaining where there must be no arbitrage, the holder of a Call option and the holder of a Put option must not derive any advantages / disadvantages from the payment of dividends. To ensure that this occurs, the detachment value is already incorporated in the option price and is therefore added to the Put and removed from the Call which expire AFTER the detachment itself.
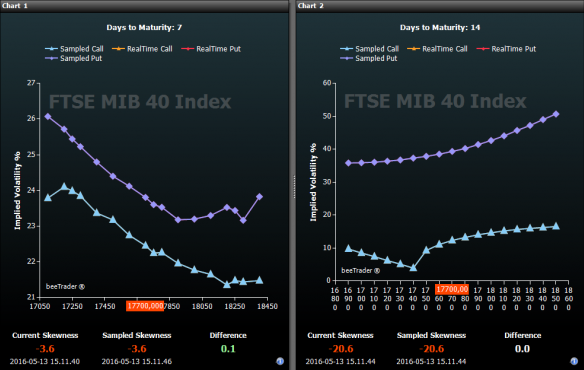
In the image it is possible to see the impact that the dividends have on volatilities: in chart 1 the volatility curve of the options with expiration the week before the detachment of dividends is represented, while in the chart 2 the volatility curve of the options is represented with expiration the week after the dividend detachment.
In Chart 2 we note a very low volatility on the ATM Call options (17700), this because the real ATM value would be 17200, the Call curve should be translated to the left of the dividend points, as well as the Put one.
Having said that, in order for the Options Strategy to be built to be correct it is necessary to align the moneyness with dividends. To do this there are two ways that are explained below: The Put-Call Parity and the inclusion of the Dividends.
Put-Call Parity
In the absence of dividends, at the price of the underlying (therefore the ATM value) the call and the put price the same risk, therefore the same premium, or the difference between the premium of a call option and the premium of a put option is equal to the difference between the current price of the underlying and the present value of the strike price of the options (leaving aside the marginal value of the interest on the capitalization).
Given this axiom, if the Options Chain is analyzed at the next maturity, the dividend gap shows how the parity of quotation between call and put is not on the ATM but more OTM towards the Put side, this because on that expiry the underlying will quote a lower price than the current one.
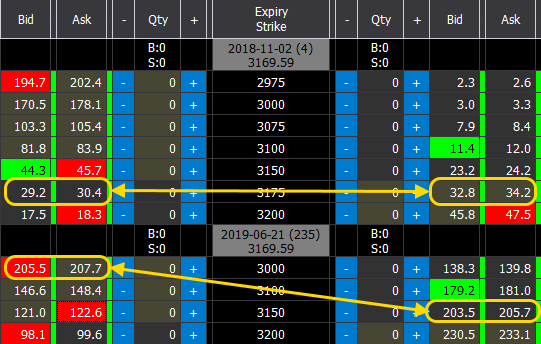
Deadline without Dividend: the calculation to arrive at the exact value is done on the ATM strike, 3175:
Call 3175: 29.2 + 30.4 / 2 = 29.8
Put 3175: 32.8 + 34.2 / 2 = 35.5
Underlying = Strike + (Call – Put), then 3175 + (29.8 – 33.5) = 3171.30
Deadline with Dividend: the calculation to arrive at the exact value is done on the ATM strike, 3150:
Call 3150: 121.0 + 122.6 / 2 = 121.8
Put 3150: 203.5 + 205.7 / 2 = 204.6
Underlying = Strike + (Call – Put), then 3150 + (121.8 – 204.6) = 3067.20
As you can see the price found on the second expiry does not correspond to the price of the underlying, this is precisely due to the effect of the dividends.
The calculation cannot be precise to the point, on the first expiry the difference between 3171.30 (obtained from the calculation) and 3169.59 (actual value) is due to the fact that we have omitted the marginal value of the interest on the capitalization and that as the price of the option we used the bid / ask average, while the actual price is not necessarily halfway.
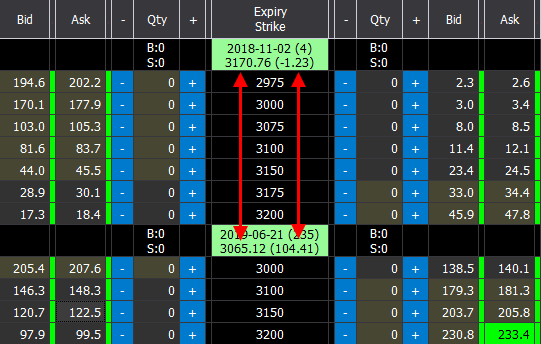
The calculation cannot be precise to the point, on the first maturity the difference between 3171.30 (obtained from the calculation) and 3169.59 (actual value) is due to the fact that we have omitted the marginal value of the interest on the capitalization and that as the price of the option we used the bid / ask average, while the actual price is not necessarily halfway.
The price of the effective underlying is shown for each expiration date of the options and in brackets the difference with the current price of the underlying, which we can attribute to the dividends that will be detached by that date.
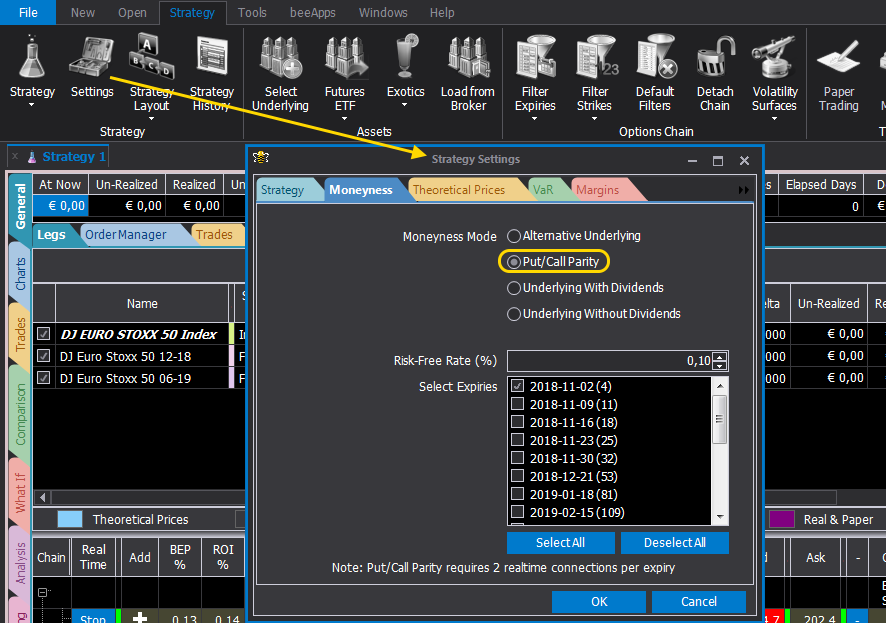
To activate the Put-Call Parity function, simply select this item in the Moneyness tab in the Strategy Settings window.
Dividends
The inclusion of dividends is very simple. From the Moneyness tab in the Strategy Settings window, once you have selected “Underlying With Dividends” (which is the default setting) click on the Dividends button and enter the dividend amount and the date.
Knowing how much the dividend amount is can be difficult. For the stocks, these are regularly published on the sites of the respective markets, while for the indices the price difference between the current price of the underlying and futures with the first expiry after the expiry of the options of interest can be used, or price difference between futures.
When dividends have been entered in the Options Strategy or the put-call parity on the payoff has been activated, the indication of the underlying’s price at expiry (green diamond) is shown, in addition to the usual indication of the current price of the underlying (red circle).
In payoffs built on underlyings that distribute dividends, in the event that the Moneyness Put / Call Parity method has been chosen or dividends have been settled to the underlying, the reference price for the calculation of the At Now curve is indicated by the red circle.
In fact, the red circle as the dividends are released will approach the green diamond. The distance between the green diamond and the red circle is equal to the sum of the dividends up to the expiry date of the strategy.
In the figure at maturity, the moneyness is given by the green diamond. This is because on expiry the red circle will coincide with the green diamond.




